Solving a quadratic program¶

Quadratic programs can be solved via the solvers.qp() function. As an example, we can solve the QP

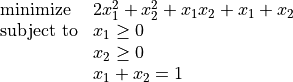
$\begin{array}{ll} \mbox{minimize} & 2x_1^2 + x_2^2 + x_1 x_2 + x_1 + x_2 \\ \mbox{subject to} & x_1 \geq 0 \\ & x_2 \geq 0 \\ & x_1 + x_2 = 1 \end{array}$

as follows:

>>> from cvxopt import matrix, solvers
>>> Q = 2*matrix([ [2, .5], [.5, 1] ])
>>> p = matrix([1.0, 1.0])
>>> G = matrix([[-1.0,0.0],[0.0,-1.0]])
>>> h = matrix([0.0,0.0])
>>> A = matrix([1.0, 1.0], (1,2))
>>> b = matrix(1.0)
>>> sol=solvers.qp(Q, p, G, h, A, b)
     pcost       dcost       gap    pres   dres
 0:  0.0000e+00  0.0000e+00  3e+00  1e+00  0e+00
 1:  9.9743e-01  1.4372e+00  5e-01  4e-01  3e-16
 2:  1.8062e+00  1.8319e+00  5e-02  4e-02  5e-16
 3:  1.8704e+00  1.8693e+00  6e-03  2e-03  1e-15
 4:  1.8749e+00  1.8748e+00  2e-04  6e-05  6e-16
 5:  1.8750e+00  1.8750e+00  2e-06  6e-07  7e-16
 6:  1.8750e+00  1.8750e+00  2e-08  6e-09  1e-15
>>> print(sol['x'])
[ 2.50e-01]
[ 7.50e-01]