Solving a linear program¶

Linear programs can be specified via the solvers.lp() function. As an example, we can solve the problem

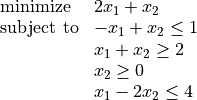
$\begin{array}{ll} \mbox{minimize} & 2x_1 + x_2 \\ \mbox{subject to} & -x_1 + x_2 \leq 1 \\ & x_1 + x_2 \geq 2 \\ & x_2 \geq 0 \\ & x_1 -2x_2 \leq 4 \end{array}$

as follows:

>>> from cvxopt import matrix, solvers
>>> A = matrix([ [-1.0, -1.0, 0.0, 1.0], [1.0, -1.0, -1.0, -2.0] ])
>>> b = matrix([ 1.0, -2.0, 0.0, 4.0 ])
>>> c = matrix([ 2.0, 1.0 ])
>>> sol=solvers.lp(c,A,b)
     pcost       dcost       gap    pres   dres   k/t
 0:  2.6471e+00 -7.0588e-01  2e+01  8e-01  2e+00  1e+00
 1:  3.0726e+00  2.8437e+00  1e+00  1e-01  2e-01  3e-01
 2:  2.4891e+00  2.4808e+00  1e-01  1e-02  2e-02  5e-02
 3:  2.4999e+00  2.4998e+00  1e-03  1e-04  2e-04  5e-04
 4:  2.5000e+00  2.5000e+00  1e-05  1e-06  2e-06  5e-06
 5:  2.5000e+00  2.5000e+00  1e-07  1e-08  2e-08  5e-08
>>> print(sol['x'])
[ 5.00e-01]
[ 1.50e+00]