L1-norm regularized least-squares¶

We consider a least-squares problem with 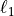$\ell_1$ -norm regularization

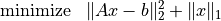
(1)¶ $\begin{array}{ll} \mbox{minimize} & \| Ax - b \|_2^2 + \| x \|_1 \end{array}$

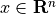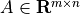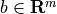with variable $x \in \mathbf{R}^n$ and problem data $A \in \mathbf{R}^{m \times n}$ and $b \in \mathbf{R}^m$ . The problem is equivalent to a QP

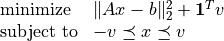
(2)¶ $\begin{array}{ll} \mbox{minimize} & \| Ax - b \|_2^2 + \mathbf{1}^Tv\\ \mbox{subject to} & -v \preceq x \preceq v \end{array}$

with 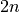$2n$ variables and 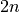$2n$ constraints. The problem can also be written as a separable QP

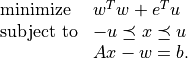
(3)¶ $\begin{array}{ll} \mbox{minimize} & w^Tw + e^Tu\\ \mbox{subject to} & -u \preceq x \preceq u \\ & Ax - w = b. \end{array}$

Documentation

Solvers for the 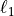$\ell_1$ -norm regularized least-squares problem are available as a Python module l1regls.py (or l1regls_mosek6.py or l1regls_mosek7.py for earlier versions of CVXOPT that use MOSEK 6 or 7). The module implements the following three functions:

l1regls(A, b)¶

Solves the problem (2) using a custom KKT solver.

Returns the solution $x$ .

l1regls_mosek(A, b)¶

Solves the problem (2) using MOSEK. This function is only available if MOSEK is installed.

Returns the solution $x$ .

l1regls_mosek2(A, b)¶

Solves the problem (3) using MOSEK. This function is only available if MOSEK is installed.

Returns the solution $x$ .

Example

from l1regls import l1regls
from cvxopt import normal

m, n = 50, 200
A, b = normal(m,n), normal(m,1)
x = l1regls(A,b)
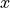