L1-norm approximation¶

The 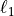$\ell_1$ -norm approximation problem is given by

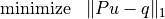
(1)¶ $\begin{array}{ll} \mbox{minimize} & \| Pu - q \|_1 \end{array}$

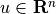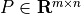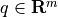with variable $u \in \mathbf{R}^n$ and problem data $P \in \mathbf{R}^{m \times n}$ and $q \in \mathbf{R}^m$ . The problem is equivalent to an LP

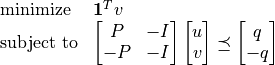
(2)¶ $\begin{array}{ll} \mbox{minimize} & \mathbf{1}^Tv \\ \mbox{subject to} & \begin{bmatrix} P & -I\\ -P & - I \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \preceq \begin{bmatrix} q \\ -q \end{bmatrix} \end{array}$

with 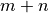$m + n$ variables and 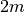$2m$ constraints. Yet another equivalent formulation is the problem

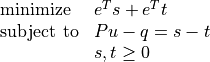
(3)¶ $\begin{array}{ll} \mbox{minimize} & e^Ts + e^Tt \\ \mbox{subject to} & Pu - q = s - t \\ & s, t \geq 0 \end{array}$

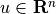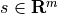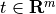with variables $u \in \mathbf{R}^n$ , $s \in \mathbf{R}^m$ , and $t \in \mathbf{R}^m$ .

Documentation

A custom solver for the 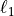$\ell_1$ -norm approximation problem is available as a Python module l1.py (or l1_mosek6.py or l1_mosek7.py for earlier versions of CVXOPT that use either MOSEK 6 or 7). The module implements the following four functions:

l1(P, q)¶

Solves the problem (2) using a custom KKT solver.

Returns the solution $u$ .

l1blas(P, q)¶

Solves the problem (2) using a custom KKT solver. This function implements the same custom KKT solver as l1(), but it uses BLAS routines instead of overloaded arithmetic.

Returns the solution $u$ .

l1mosek(P, q)¶

Solves the problem (2) using MOSEK. This function is only available if MOSEK is installed.

Returns the solution $u$ .

l1mosek2(P, q)¶

Solves the problem (3) using MOSEK. This function is only available if MOSEK is installed.

Returns the solution $u$ .

Example

from l1 import l1
from cvxopt import normal

m, n = 500, 100
P, q = normal(m,n), normal(m,1)
u = l1(P,q)