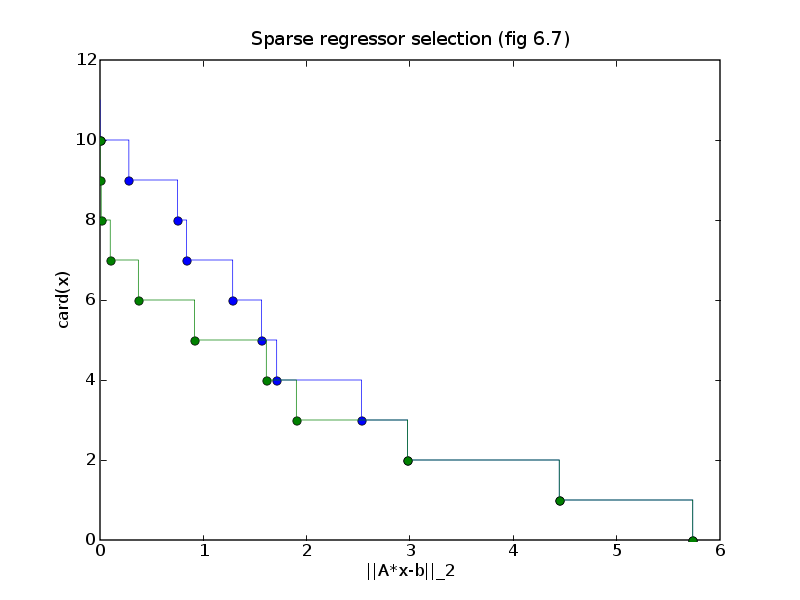
# Figure 6.7, page 311.
# Sparse regressor selection.
#
# The problem data are different from the book.
from cvxopt import blas, lapack, solvers, matrix, mul
from pickle import load
solvers.options['show_progress'] = 0
try: import pylab
except ImportError: pylab_installed = False
else: pylab_installed = True
data = load(open('regsel.bin','rb'))
A, b = data['A'], data['b']
m, n = A.size
# In the heuristic, set x[k] to zero if abs(x[k]) <= tol * max(abs(x)).
tol = 1e-1
# Data for QP
#
# minimize (1/2) ||A*x - b|_2^2
# subject to -y <= x <= y
# sum(y) <= alpha
P = matrix(0.0, (2*n,2*n))
P[:n,:n] = A.T*A
q = matrix(0.0, (2*n,1))
q[:n] = -A.T*b
I = matrix(0.0, (n,n))
I[::n+1] = 1.0
G = matrix([[I, -I, matrix(0.0, (1,n))], [-I, -I, matrix(1.0, (1,n))]])
h = matrix(0.0, (2*n+1,1))
# Least-norm solution
xln = matrix(0.0, (n,1))
xln[:m] = b
lapack.gels(+A, xln)
nopts = 100
res = [ blas.nrm2(b) ]
card = [ 0 ]
alphas = blas.asum(xln)/(nopts-1) * matrix(range(1,nopts), tc='d')
for alpha in alphas:
# minimize ||A*x-b||_2
# subject to ||x||_1 <= alpha
h[-1] = alpha
x = solvers.qp(P, q, G, h)['x'][:n]
xmax = max(abs(x))
I = [ k for k in range(n) if abs(x[k]) > tol*xmax ]
if len(I) <= m:
xs = +b
lapack.gels(A[:,I], xs)
x[:] = 0.0
x[I] = xs[:len(I)]
res += [ blas.nrm2(A*x-b) ]
card += [ len(I) ]
# Eliminate duplicate cardinalities and make staircase plot.
res2, card2 = [], []
for c in range(m+1):
r = [ res[k] for k in range(len(res)) if card[k] == c ]
if r:
res2 += [ min(r), min(r) ]
card2 += [ c, c+1 ]
# if pylab_installed:
# pylab.figure(1, facecolor='w')
# pylab.plot( res2[::2], card2[::2], 'o')
# pylab.plot( res2, card2, '-')
# pylab.xlabel('||A*x-b||_2')
# pylab.ylabel('card(x)')
# pylab.title('Sparse regressor selection (fig 6.7)')
# print("Close figure to start exhaustive search.")
# pylab.show()
# Exhaustive search.
def patterns(k,n):
"""
Generates all 0-1 sequences of length n with exactly k nonzeros.
"""
if k==0:
yield n*[0]
else:
for x in patterns(k-1,n-1): yield [1] + x
if k <= n-1:
for x in patterns(k,n-1): yield [0] + x
bestx = matrix(0.0, (n, m)) # best solution for each cardinality
bestres = matrix(blas.nrm2(b), (1, m+1)) # best residual
x = matrix(0.0, (n,1))
for k in range(1,m):
for s in patterns(k,n):
I = [ i for i in range(n) if s[i] ]
st = ""
for i in s: st += str(i)
print("%d nonzeros: " %k + st)
x = +b
lapack.gels(A[:,I], x)
res = blas.nrm2(b - A[:,I] * x[:k])
if res < bestres[k]:
bestres[k] = res
bestx[:,k][I] = x[:k]
bestres[m] = 0.0
if pylab_installed:
pylab.figure(1, facecolor='w')
# heuristic result
pylab.plot( res2[::2], card2[::2], 'o' )
pylab.plot( res2, card2, '-')
# exhaustive result
res2, card2 = [ bestres[0] ], [ 0 ]
for k in range(1,m+1):
res2 += [bestres[k-1], bestres[k]]
card2 += [ k, k]
pylab.plot( bestres.T, range(m+1), 'go')
pylab.plot( res2, card2, 'g-')
pylab.xlabel('||A*x-b||_2')
pylab.ylabel('card(x)')
pylab.title('Sparse regressor selection (fig 6.7)')
pylab.show()